SISTEMA DE NUMERAÇÃO BINÁRIO
O sistema decimal é muito usado no cotidiano, pois nos oferece uma forma mais simples de manipular os números em determinadas situações matemáticas, é composto por dez números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
O uso da Matemática em situações diversas não diz respeito somente ao homem, os computadores utilizam números para efetuar cálculos complexos com uma maior rapidez e praticidade. O sistema binário é usado pelos computadores é e constituído de dois dígitos o 0 e o 1. A combinação desses dígitos leva o computador a criar várias informações: letras, palavras, textos, cálculos.
A criação do sistema de numeração binária é atribuída ao matemático alemão Leibniz.
Numeração Binária e Numeração Decimal
Transformando decimal em binário
14(base10) = 1110(base2)
14 / 2 = 7 resto 0
7 / 2 = 3 resto 1
3 / 2 = 1 resto 1
36(base10) = 100100(base2)
36 / 2 = 18 resto 0
18 / 2 = 9 resto 0
9 / 2 = 4 resto 1
4 / 2 = 2 resto 0
2 / 2 = 1 resto 0
O número binário será formado agrupando o último resultado seguido dos restos das divisões anteriores.
Transformando binário em decimal
110100(base2) = 52 (base10)
O uso da Matemática em situações diversas não diz respeito somente ao homem, os computadores utilizam números para efetuar cálculos complexos com uma maior rapidez e praticidade. O sistema binário é usado pelos computadores é e constituído de dois dígitos o 0 e o 1. A combinação desses dígitos leva o computador a criar várias informações: letras, palavras, textos, cálculos.
A criação do sistema de numeração binária é atribuída ao matemático alemão Leibniz.
Numeração Binária e Numeração Decimal
Transformando decimal em binário
14(base10) = 1110(base2)
14 / 2 = 7 resto 0
7 / 2 = 3 resto 1
3 / 2 = 1 resto 1
36(base10) = 100100(base2)
36 / 2 = 18 resto 0
18 / 2 = 9 resto 0
9 / 2 = 4 resto 1
4 / 2 = 2 resto 0
2 / 2 = 1 resto 0
O número binário será formado agrupando o último resultado seguido dos restos das divisões anteriores.
Transformando binário em decimal
110100(base2) = 52 (base10)
1
|
1
|
0
|
1
|
0
|
0
|
casa 6
|
casa 5
|
casa 4
|
casa 3
|
casa 2
|
casa 1
|
25
|
24
|
23
|
22
|
21
|
20
|
1 x 25
|
1 x 24
|
0 x 23
|
1 x 22
|
0 x 21
|
0 x 20
|
1 x 32
|
1 x 16
|
0 x 8
|
1 x 4
|
0 x 2
|
0 x 1
|
32
|
16
|
0
|
4
|
0
|
0
|
32 + 16 + 0 + 4 + 0 + 0 = 52
1100100(base2) = 100(base10)
1
|
1
|
0
|
0
|
1
|
0
|
0
|
casa 7
|
casa 6
|
casa 5
|
casa 4
|
casa 3
|
casa 2
|
casa 1
|
26
|
25
|
24
|
23
|
22
|
21
|
20
|
1 x 26
|
1 x 25
|
0 x 24
|
0 x 23
|
1 x 22
|
0 x 21
|
0 x 20
|
1 x 64
|
1 x 32
|
0 x 16
|
0 x 8
|
1 x 4
|
0 x 2
|
0 x 1
|
64
|
32
|
0
|
0
|
4
|
0
|
0
|
64 + 32 + 0 + 0 + 4 + 0 +0 = 100
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
VÍDEO AULA CLIQUE NO LINK:http://www.youtube.com/watch?v=qSVHUA6w1vE
Na computação, os algarismos 0 e 1 do sistema binário são usados para representar quantidades mínimas de informação, chamadas bits.
O termo bit deriva do inglês binary digit (dígito binário). Em geral, quando escrevemos os números no sistema binário gastamos mais bits do que a quantidade de dígitos que gastaríamos no sistema decimal; por exemplo, 1 024, que é escrito com 4 dígitos no sistema decimal, tem 11 bits no binário. Esse fato, que constituiria um enorme problema para a capacidade limitada de memória do homem, não é um problema para o computador, que possui uma enorme capacidade de armazenamento de dados.
 , bem como
, bem como  . A escolha da melhor representação irá depender de como o número será utilizado ou de quais operações serão realizadas.
. A escolha da melhor representação irá depender de como o número será utilizado ou de quais operações serão realizadas.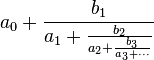 , em que o primeiro termo,
, em que o primeiro termo,  , é um número inteiro e os demais números
, é um número inteiro e os demais números 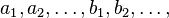 são números inteiros positivos.
são números inteiros positivos. , em que todos os números
, em que todos os números 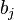 são iguais a 1. Uma expressão da forma
são iguais a 1. Uma expressão da forma  é uma fração continuada simples finita.
é uma fração continuada simples finita. na forma de fração continuada.
na forma de fração continuada.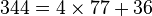 . Logo,
. Logo,  .
. . Com isso, obtém-se a expressão
. Com isso, obtém-se a expressão 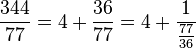 .
. .
. .
.
.jpg)


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)















.jpg)
