Conjuntos Numéricos
Conjunto dos Números Naturais
São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N.
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:
- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z-:
Aqui, vamos dar dicas de como achar as frações geratrizes de dízimas periódicas simples e compostas, de uma forma bem prática.
Período: 2
Coloca-se o período no numerador da fração e, para cada algarismo dele, coloca-se um algarismo 9 no denominador.
Nesse caso, temos uma dízima simples e a parte inteira diferente de zero.
Uma estratégia é separar parte inteira e parte decimal:
Aqui, a dica é um pouco diferente: para cada algarismo do período ainda se coloca um algarismo 9 no denominador. Mas, agora, para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador.
No caso do numerador, faz-se a seguinte conta:
(parte inteira com antiperíodo e período) - (parte inteira com antiperíodo)
Assim:
b) 1,64444...
c) 21,308888... (o período tem 1 algarismo e o antiperíodo tem 2 algarismos)
d) 2,4732121212... (o período tem 2 algarismos e o antiperíodo tem 3 algarismos)
Por que dá certo?
Veja a explicação na forma como geralmente se aprende a achar a fração geratriz na escola:
Chama-se a fração geratriz de x:
Para achar o valor de x, encontram-se múltiplos dele com apenas o período na parte decimal
E subtraem-se as duas igualdades
Assim, cria-se uma equação e elimina-se a parte infinita dos números envolvidos, achando-se a fração geratriz.
Note que, no método mais prático, a conta sugerida é a mesma que aparece na equação: 164 - 16, e o denominador fica exatamente com os mesmos algarismos.
No caso do exemplo D, deve-se multiplicar x por números ainda maiores, para se achar a mesma parte decimal nos dois números a serem subtraídos:
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:
N = {0,1,2,3,4,5,6,7,8,9,10, ...}
N* = {1,2,3,4,5,6,7,8,9,10,11, ...}
N* = {1,2,3,4,5,6,7,8,9,10,11, ...}
Conjunto dos Números Inteiros
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:
Z = {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
O conjunto dos inteiros possui alguns subconjuntos, eles são:
- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
Z+ = {0,1,2,3,4,5,6, ...}
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {..., -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não-nulos
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
Z*+ = {1, 2, 3, 4, 5, 6, 7, ...}
Z*+ = N*
- Inteiros não positivos e não nulos
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
Z*- = {... -4, -3, -2, -1}
Conjunto dos Números Racionais
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como "12,050505...", são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como "12,050505...", são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.
A representação da fração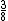 
em números decimais é 0,375, assim como a representação decimal da fração 
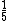é 0,2.
Repare que embora o número de casas decimais em cada um dos exemplos seja diferente, eles são finitos. O primeiro exemplo possui três casas decimais, ao passo que o segundo exemplo possui apenas uma.
Agora qual seria a representação decimal da fração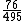 
?
Note que neste caso o número de casas decimais da representação desta fração na forma decimal, não será um número finito. 76 dividido por 495 será algo como 0,1535353...
Se continuarmos o processo de divisão, iremos indefinidamente acrescentar um dígito 5, depois um 3, depois um 5 e assim por diante, sendo que sempre poderemos continuar acrescentando mais um dígito. A isto damos o nome de dízima periódica
As dízimas periódicas podem ser simples ou composta, no caso do exemplo acima temos uma dízima periódica composta.
A dízima periódica composta 0,1535353... foi gerada a partir da fração 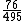, por isto esta fração é chamada defração geratriz da dízima periódica.
Classificando as Dízimas Periódicas em Simples e Compostas
A dízima periódica 0,1535353... é composta, pois ela possui um anteperíodo que não se repete, no caso o número1, e um período formado pelo número 53, que se repete indefinidamente. Se fosse apenas 0,535353... teríamos uma dízima periódica simples, pois ela possui apenas um período, 53, mas não um anteperíodo.
Veja abaixo alguns exemplos:
Exemplos de Dízimas Periódicas Simples
0,111... período igual a 1
0,252525... período igual a 25
0,010101... período igual a 01
0,123123123... período igual a 123
Exemplos de Dízimas Periódicas Compostas
0,2333... anteperíodo igual a 2 e período igual a 3
0,45222... anteperíodo igual a 45 e período igual a 2
0,171353535... anteperíodo igual a 171 e período igual a 35
0,32101230123... anteperíodo igual a 32 e período igual a 0123
Fração geratriz
Como achar a fração geratriz de uma dízima periódica?
A fração geratriz é aquela que dá origem a uma dízima periódica.
Aqui, vamos dar dicas de como achar as frações geratrizes de dízimas periódicas simples e compostas, de uma forma bem prática.
Dízimas periódicas simples
a) 0,2222...Período: 2
Coloca-se o período no numerador da fração e, para cada algarismo dele, coloca-se um algarismo 9 no denominador.
 |
 |
Nesse caso, temos uma dízima simples e a parte inteira diferente de zero.
Uma estratégia é separar parte inteira e parte decimal:
 |
Dízimas periódicas compostas
a) 0,27777...Aqui, a dica é um pouco diferente: para cada algarismo do período ainda se coloca um algarismo 9 no denominador. Mas, agora, para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador.
No caso do numerador, faz-se a seguinte conta:
(parte inteira com antiperíodo e período) - (parte inteira com antiperíodo)
Assim:
 |
b) 1,64444...
 |
c) 21,308888... (o período tem 1 algarismo e o antiperíodo tem 2 algarismos)
 |
d) 2,4732121212... (o período tem 2 algarismos e o antiperíodo tem 3 algarismos)
 |
Por que dá certo?
Veja a explicação na forma como geralmente se aprende a achar a fração geratriz na escola:
Chama-se a fração geratriz de x:
 |
Para achar o valor de x, encontram-se múltiplos dele com apenas o período na parte decimal
 |
E subtraem-se as duas igualdades
 |
Assim, cria-se uma equação e elimina-se a parte infinita dos números envolvidos, achando-se a fração geratriz.
Note que, no método mais prático, a conta sugerida é a mesma que aparece na equação: 164 - 16, e o denominador fica exatamente com os mesmos algarismos.
No caso do exemplo D, deve-se multiplicar x por números ainda maiores, para se achar a mesma parte decimal nos dois números a serem subtraídos:
 |
*Michele Viana Debus de França é licenciada em matemática pela USP e mestre em educação matemática pela PUC-SP.
Nenhum comentário:
Postar um comentário